MCD RedesNeuronales Proyecto

Documento con conceptos y matemáticas empleadas en las redes neuronales, incluído un ejemplo práctico.

Realizar un escrito con los siguiente cuatro puntos:

Definición y ejemplos de lo que es una red neuronal

Esquema General de las matemáticas que involucran las redes neuronales con sus respectivos diagramas de flujo.

Elegir un problema de nuestro interés

Desarrollo matemático amplio y detallado de las matemáticas que se usan en el problema, usando dicha red neuronal.

1. Definición y ejemplos de Redes Neuronales

1.1 Definición

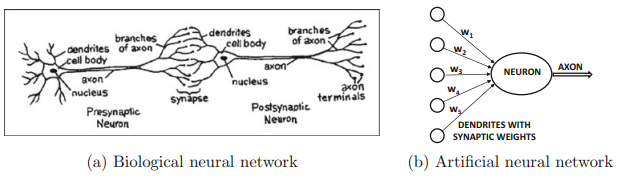
Las redes neuronales artificiales son técnicas populares de aprendizaje automático que simulan el mecanismo de aprendizaje en organismos biológicos. El sistema nervioso humano contiene células que se conocen como neuronas. Las neuronas están conectadas entre sí mediante el uso de axones y dendritas, y las regiones de conexión entre axones y dendritas se denominan sinapsis. Las conexiones sinápticas a menudo cambian su fortaleza en respuesta a estímulos externos. Este cambio es cómo ocurre el aprendizaje en los organismos vivos. Este mecanismo biológico se simula en redes neuronales artificiales, que contienen unidades de cálculo que se conocen como neuronas. Las unidades de cálculo están conectadas entre sí mediante pesos, que desempeñan el mismo papel que las fortalezas de las conexiones sinápticas en los organismos biológicos. Cada entrada a una neurona se escala con un peso, que afecta a la función calculada en esa unidad.

1.2. Ejemplos

Existen varias arquitecturas de redes neuronales. Las más comunes son:

1.2.1 Perceptron

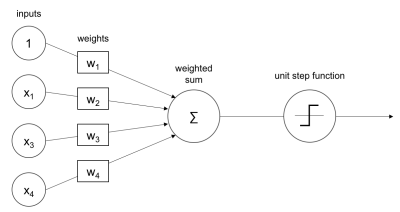
Una neurona artificial, o perceptrón, toma varias entradas y realiza una suma ponderada para producir una salida. El peso del perceptron es determinado durante el proceso de entrenamiento y es basado en los datos que se usaron para entrenarlo.

1.2.2 Perceptrón Multicapa

La siguiente imagen es un perceptrón multicapa.

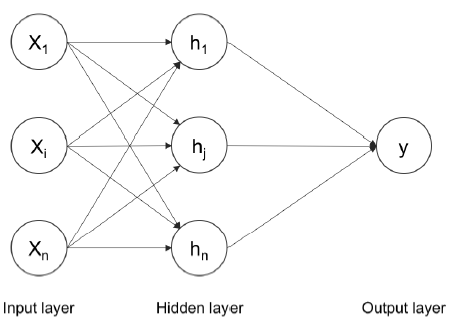
Varias entradas de x pasan a través de una capa oculta de perceptrones y son sumadas para la salida. El teorema universal de aproximación sugiere que una red neuronal puede aproximar cualquier función. La capa oculta tambien puede ser conocida como capa densa (dense layer). Cada capa puede tener una función de activación (que puede ser distinta o no). El número de capas ocultas y de perceptrones puede ser elegido en base al problema a resolver.

Una red perceptrón multicapa puede ser usada para problemas de clasificación multi-clase. Un problema de clasificación multi-clase (multi-class classification problem) trata de discriminar más de 10 categorías.

1.2.3 Redes Neuronales Convolucionales

Las redes neuronales convolucionales (CNNs) al igual que las ANN normales tienen pesos, bias y salidas mediante una activación no-lineal.

Las redes neuronales regulares toman entradas y las neuronas se conectan completamente (fully connected) a las siguientes capas. Las neuronas dentro de la misma capa no comparten ninguna conexión.

Si usamos redes neuronales regulares para imágenes, por ejemplo, van a terminar siendo muy grandes en tamaño debido al gran número de neuronas y, como consecuencia, en sobreentrenamiento. Es por eso que este tipo de redes no deben de usarse para entrenarse con imágenes, debido a que las imágenes son muy grandes en tamaño. Al incrementarse el tamaño del modelo, se requiere un enorme número de neuronas.

Una imagen puede ser considerada como un volumen con dimensiones de altura, anchura y profundidad. La profundidad es el canal de la imágen, la cual si es a color suele ser RGB (red,blue,green).

Las neuronas de una CNN están dispuestas de forma volumétrica para aprovechar el volumen. Cada una de las capas transforma el volumen de entrada en un volumen de salida:

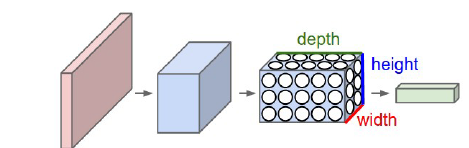
Los filtros de red neuronal convolucional codifican (encode) por transformación. Los filtros aprendidos detectan características o patrones en las imágenes. Cuanto más profunda es la capa, más abstracto es el patrón. Algunos análisis han demostrado que estas capas tienen la capacidad de detectar bordes, esquinas y patrones.

1.2.4 Redes Neuronales Recurrentes

Las RNN pueden modelar información sequencial. Ellas no asumen que los data points son intensivos. Las RNN realizan la misma tarea desde el output de los datos previos de una serie de datos secuencial. Esto puede ser pensdo o catalogado como si tuviesen “memoria”. Las RNN no pueden recordar secuencias o tiempos más largos. Se despliega durante el proceso de entrenamiento, como se muestra en la siguiente imagen:

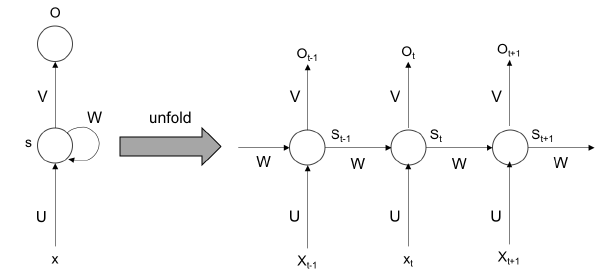
Como se muestra en la imagen, durante cada iteración se despliega y se entrena cada vez. Durante el back-prop (propagación hacia atrás), los gradientes pueden desaparecer con el tiempo. Para atacar este problema, existen las LSTM para recordar en un periodo más largo del tiempo.

1.2.5 Redes Generativas Antagónicas

Son utilizadas en la generación de contenido nuevo y realista, como imágenes, música y texto. Se componen de dos redes: el generador, que crea muestras sintéticas, y el discriminador, que evalúa si las muestras son reales o falsas. Recientemente han ganado popularidad por ser la base de motores de AI para generar y procesar imágenes.

1.3 Aplicaciones

1.3.1 Computer Vision

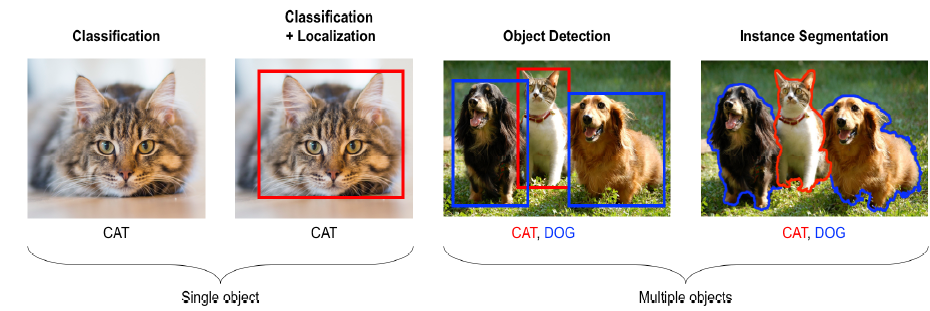
La visión por computadora permite que las computadoras adopten la posibilidad de ver como los humanos. Los diferentes problemas que son propios de la visión artificial puede ser atacados y resueltos efectivamente con técnicas de deep learning. Entre las principales aplicaciones, podemos encontrar problemas de clasificación de imágenes, detección y segmentación de objetos, o incluso analizar videos.

1.3.2 Natural Language Processing

El procesamiento del lenguaje natural (PLN) es una rama de la inteligencia artificial y la lingüística computacional que se ocupa de la interacción entre las computadoras y el lenguaje humano. Su objetivo principal es permitir que las computadoras comprendan, interpreten y generen lenguaje humano de manera similar a como lo hacen los seres humanos.

Las redes neuronales se usan en estos ejemplos para traducción automática de videos, análisis de sentimientos en textos o artículos/comentarios de opinión, así como generación automática de texto.

1.3.3 Time Series

El deep learning ha demostrado ser efectivo en el análisis y predicción de series de tiempo. Algunas aplicaciones específicas incluyen pronósticos de clima, finanzas o mercado financiero. También se puede usar en marketing para ver la predicción de oferta/demanda, e incluso para Transporte y vía pública donde se puede predecir cantidad de tráfico y el flujo de vehículos.

2. Esquema General de las matemáticas que involucran las redes neuronales

En cuanto a las matemáticas que se usan para las redes neuronales es una combinación entre Algebra Lineal, Probabilidad y Estadística, Cálculo de varias variables y optimización.

2.1 Algebra Lineal

El álgebra lineal es el cimiento del aprendizaje automático y el aprendizaje profundo. El álgebra lineal nos brinda los fundamentos matemáticos para resolver las ecuaciones que utilizamos para construir modelos. Veamos algunos conceptos básicos:

2.1.1 Escalar

En matemáticas, cuando se menciona el término escalar, nos referimos a elementos en un vector. Un escalar es un número real y un elemento de un campo usado para definir un vector espacio.

En informática, el término escalar es sinónimo del término variable y es una ubicación de almacenamiento emparejada con un nombre simbólico. Esta ubicación de almacenamiento contiene una cantidad desconocida de información llamada valor

2.1.2 Vector

Para nuestro uso, definimos un vector de la siguiente manera:

Para un entero positivo n, un vector es una n-tupla, conjunto (múltiple) ordenado o matriz de n números, llamados elementos o escalares.

Lo que estamos diciendo es que queremos crear una estructura de datos llamada vector a través de un proceso llamado vectorización. El número de elementos en el vector se denomina "orden" (o "longitud") del vector. Los vectores también pueden representar puntos en un espacio n-dimensional.

En el sentido espacial, la distancia euclidiana desde el origen hasta el punto representado por el vector nos da la "longitud" del vector.

En textos matemáticos, a menudo vemos vectores escritos de la siguiente manera:

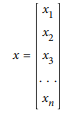
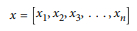
Siendo el primero catalogado como “vector columna” y el segundo como “vector renglón”.

2.1.3 Matriz

Considere una matriz como un grupo de vectores que tienen todos la misma dimensión (número de columnas). De esta forma una matriz es un arreglo bidimensional para el cual tenemos filas y columnas.

Si se dice que nuestra matriz es una matriz n × m, tiene n filas y m columnas. Las matrices son una estructura central en álgebra lineal y aprendizaje automático.

2.1.4 Tensor

Un tensor es una matriz multidimensional en el nivel más fundamental. Es una estructura matemática más general que un vector. Podemos ver un vector simplemente como una subclase de tensores.

Con tensores, las filas se extienden a lo largo del eje y y las columnas a lo largo del eje x. Cada eje es una dimensión y los tensores tienen dimensiones adicionales. Los tensores también tienen un rango. Comparativamente, un escalar es de rango 0 y un vector es de rango 1. También vemos que una matriz es de rango 2. Cualquier entidad de rango 3 y superior se considera un tensor.

2.1.5 Hiperplano

Otro objeto de álgebra lineal que debe tener en cuenta es el hiperplano. En el campo de la geometría, el hiperplano es un subespacio de una dimensión menor que su espacio ambiental. En un espacio tridimensional, los hiperplanos tendrían dos dimensiones. En el espacio bidimensional, consideramos que una línea unidimensional es un hiperplano.

Un hiperplano es una construcción matemática que divide un espacio n dimensional en "partes" separadas y, por lo tanto, es útil en aplicaciones como la clasificación. La optimización de los parámetros del hiperplano es un concepto central en el modelado lineal.

2.1.6 Producto Punto

Una operación básica de álgebra lineal que vemos a menudo en el aprendizaje automático es el producto punto. El producto punto a veces se denomina "producto escalar" o "producto interno". El producto punto toma dos vectores de la misma longitud y devuelve un solo número. Esto se hace haciendo coincidir las entradas en los dos vectores, multiplicándolos y luego sumando los productos así obtenidos. Es importante mencionar que este solo número codifica una gran cantidad de información.

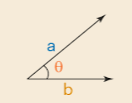
Para empezar, el producto escalar es una medida del tamaño de los elementos individuales en cada vector. Dos vectores con valores bastante grandes pueden dar resultados bastante grandes, y dos vectores con valores bastante pequeños pueden dar valores bastante pequeños. Cuando los valores relativos de estos vectores se contabilizan matemáticamente con algo llamado normalización, el producto escalar es una medida de cuán similares son estos vectores. Esta noción matemática de un producto escalar de dos vectores normalizados se llama similitud de coseno.

2.1.7 Producto Hadamard (elemento-a-elemento)

Otra operación común de álgebra lineal que vemos en la práctica es el producto de elementos (o el "producto Hadamard"). Esta operación toma dos vectores de la misma longitud y produce un vector de la misma longitud con cada elemento correspondiente multiplicado entre los dos vectores fuente.

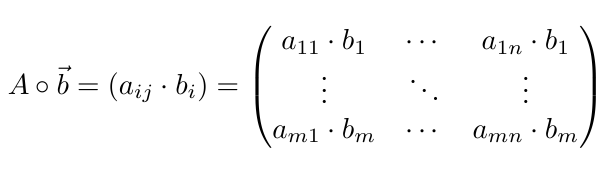
2.1.8 Producto Exterior

Esto se conoce como el "producto tensorial" de dos vectores de entrada. Tomamos cada elemento de un vector columna y lo multiplicamos por todos los elementos en un vector fila creando una nueva fila en la matriz resultante

2.1.9 Sistema de Ecuaciones

En el mundo del álgebra lineal nos interesa resolver sistemas de ecuaciones lineales de la forma:

Ax = b

donde A es una matriz de nuestro conjunto de vectores de fila de entrada y b es el vector de columna de etiquetas para cada vector en la matriz A.

Cada valor independiente de la matriz A es considerado como característica (feature) de nuestros datos de entrada. Una característica es cualquier valor de columna en la matriz de entrada A que estamos usando como variable independiente. Las características se pueden tomar directamente de los datos de origen, pero la mayoría de las veces vamos a usar algún tipo de transformación para obtener los datos de entrada sin procesar en una forma que sea más apropiada para el modelado.

2.2 Probabilidad y Estadística

Algunos de los conceptos básicos en la Estadística son:

Probabilidad

Distribuciones

Existen otras relaciones básicas que se usan en la Estadística Descriptiva y la Estadística Inferencial. Dentro de la Estadística Descriptiva tenemos:

Histogramas

Boxplots (Diagrama de Cajas y Bigotes)

Scatterplot (Diagrama de Dispersión)

Media

Desviación Estandar

Coeficiente de Correlación

Esto contrasta con la forma en que las estadísticas inferenciales se ocupan de las técnicas para generalizar de una muestra a una población. Estos son algunos ejemplos de estadística inferencial:

p-values

Intervalos de Confianza

2.2.1 Probabilidad

Definimos probabilidad de un evento E como un número siempre entre 0 y 1. En este contexto, el valor 0 infiere que el evento E no tiene posibilidad de ocurrir, y el valor 1 significa que el evento E seguramente ocurrirá. Muchas veces veremos esta probabilidad expresada como un número decimal, pero también podemos expresarla como un porcentaje entre 0 y 100%; no veremos probabilidades válidas inferiores al 0 por ciento y superiores al 100 por ciento.

El ejemplo más clásico es el de lanzar una moneda al aire. Podemos expresar la probabilidad de un evento de la siguiente manera

P(E) = 0.5

La probabilidad está en el centro de las redes neuronales y el deep learning debido a su papel en la extracción y clasificación de características, dos de las funciones principales de las redes neuronales profundas.

2.2.2 Probabilidad Condicional

Cuando queremos saber la probabilidad de un evento dado en base a la presencia existente de que ocurra otro evento, expresamos esto como una probabilidad condicional. Esto se expresa en la literatura en la forma:

P(E|F)

donde:

E es el evento para el cual estamos interesados en una probabilidad.

F es el evento que ya ha ocurrido

A veces, escucharemos el segundo evento, F, referido como la "condición". La probabilidad condicional es interesante en el aprendizaje automático y el aprendizaje profundo porque a menudo nos interesa saber cuándo suceden varias cosas y cómo interactúan. Estamos interesados en las probabilidades condicionales en el aprendizaje automático en el contexto en el que aprenderíamos un clasificador aprendiendo

P(E|F)

donde E es nuestra etiqueta y F es un número de atributos sobre la entidad para la que estamos prediciendo E.

2.2.3 Teorema de Bayes

Una de las aplicaciones más comunes de las probabilidades condicionales es el teorema de Bayes (o fórmula de Bayes). En el campo de la medicina, lo vemos utilizado para calcular la probabilidad de que un paciente que da positivo en una prueba para una enfermedad específica realmente tenga la enfermedad.

Definimos la fórmula de Bayes para dos eventos cualesquiera, A y B, como

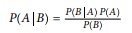
2.2.4 Distribuciones

Una distribución de probabilidad es una especificación de la estructura estocástica de las variables aleatorias. En estadística, nos basamos en hacer suposiciones sobre cómo se distribuyen los datos para hacer inferencias sobre los datos.

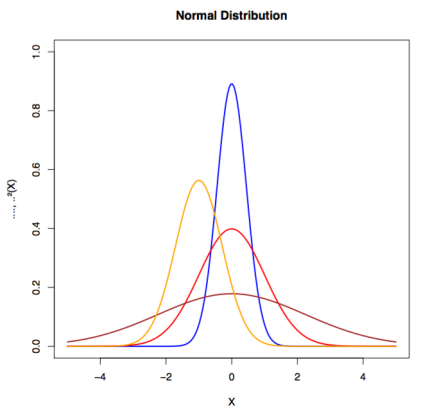
Queremos una fórmula que especifique qué tan frecuentes son los valores de las observaciones en la distribución y cómo los valores pueden ser tomados por puntos en la distribución. Una distribución común se conoce como distribución normal (también llamada distribución gaussiana o curva de campana). Nos gusta ajustar un conjunto de datos a una distribución porque si el conjunto de datos está razonablemente cerca de la distribución, podemos hacer suposiciones basadas en la distribución teórica sobre cómo operamos con los datos.

Clasificamos las distribuciones en continuas o discretas. Una distribución discreta tiene datos que pueden asumir solo ciertos valores. En una distribución continua, los datos pueden ser cualquier valor dentro del rango. Un ejemplo de una distribución continua sería la distribución normal. Un ejemplo de distribución discreta sería la distribución binomial.

2.3 Cálculo y Optimización

Fundamentalmente, el aprendizaje automático se basa en técnicas algorítmicas para minimizar el error en esta ecuación a través de la optimización.

En optimización, nos enfocamos en cambiar los números en el vector de columna x (vector de parámetros) hasta que encontremos un buen conjunto de valores que nos brinde los resultados más cercanos a los valores reales. Cada peso en la matriz de peso se ajustará después de que la función de pérdida calcule el error (basado en el resultado real, como el vector de la columna b) producido por la red. Una matriz de error que atribuya una parte de la pérdida a cada peso se multiplicará por los pesos mismos.

2.3.1 Regresión

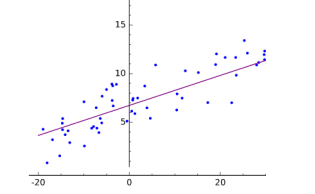
La regresión se refiere a funciones que intentan predecir una salida de valor real. Este tipo de función estima la variable dependiente conociendo la variable independiente. La clase de regresión más común es la regresión lineal. La regresión lineal intenta generar una función que describa la relación entre x e y y, para valores conocidos de x, predice valores de y que resultan ser precisos.

y = a + Bx

donde a es la intersección con y, B son las características de entrada y x es el vector de parámetros

2.3.2 Optimización

El proceso antes mencionado de ajustar pesos para producir conjeturas cada vez más precisas sobre los datos se conoce como optimización de parámetros. Puedes pensar en este proceso como un método científico. Formulamos una hipótesis, la comparamos con la realidad y refinamos o reemplazamos esa hipótesis una y otra vez para describir mejor los eventos en el mundo.

Cada conjunto de pesos representa una hipótesis específica sobre lo que significan las entradas; es decir, cómo se relacionan con los significados contenidos en las etiquetas de uno.

Los conceptos más importantes en la optimización aplicada al aprendizaje automático son:

Parámetros: Transformar la entrada para ayudar a determinar las clasificaciones que infiere la red

Loss function: Mide qué tan bien clasifica (minimiza el error) en cada paso

Función de Optimización: Guía hacia los puntos de menor error.

2.3.3 Descenso de Gradiente

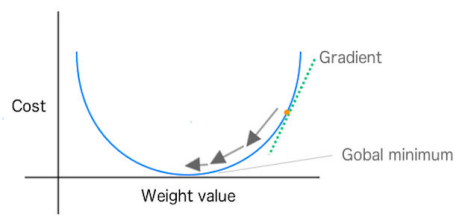
En el descenso de gradiente, podemos imaginar la calidad de las predicciones de nuestra red (en función de los valores de peso/parámetro) como un paisaje. Las colinas representan ubicaciones (valores de parámetros o pesos) que dan mucho error de predicción; los valles representan ubicaciones con menos error. Elegimos un punto en ese paisaje en el que colocar nuestro peso inicial. Luego, podemos seleccionar el peso inicial en función del conocimiento del dominio (si estamos entrenando una red para clasificar una especie de flor, sabemos que la longitud de los pétalos es importante, pero el color no lo es). O, si dejamos que la red haga todo el trabajo, podemos elegir los pesos iniciales al azar

El propósito es mover ese peso cuesta abajo, a áreas de menor error, lo más rápido posible. Un algoritmo de optimización como el descenso de pendiente puede detectar la pendiente real de las colinas con respecto a cada peso; es decir, sabe en qué dirección está abajo. El descenso de gradiente mide la pendiente (el cambio en el error causado por un cambio en el peso) y lleva el peso un paso hacia el fondo del valle. Lo hace tomando una derivada de la función de pérdida para producir el gradiente. El gradiente da la dirección para el siguiente paso en el algoritmo de optimización.

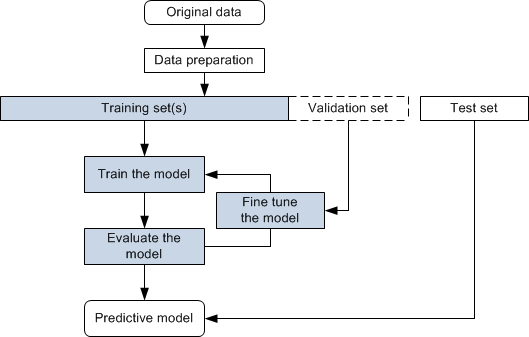
2.4 Workflow de Deep Learning

Existen 10 asos que siempre se deben de seguir al momento de trabajar con redes neuronales, donde toma como base el método científico:

Definición del problema

Recolección de los datos

Procesar los datos

Definir los datos de entrenamiento y datos de prueba

Definir un modelo de red neuronal

Configurar el proceso de aprendizaje

Inicializar los pesos y sesgos

Entrenar al modelo

Validar el modelo

Usar el modelo

3. Descripción del Problema: Clasificación de números escritos a mano usando el dataset MNIST

3.1 Definición

El dataset MNIST (Modified National Institute of Standards and Technology) o MNIST Database, en una base de datos que contiene una recopilación de números (dígitos) escritos a mano. Este conjunto fue creado a partir de un re-muestreo de un conjunto previo conocido como NIST.

3.2 Historia del MNIST

National Institute of Standards and Technology (NIST) es un instituto en los Estados Unidos, cuya misión es promover la innovación y la competencia industrial en el país. Como parte de esta misión, los científicos e ingenieros del NIST continuamente refinan la ciencia de la medición (metrología) y utilizan grandes bases de datos para su continua experimentación.

El conjunto de imágenes en el MNIST database fue creado en 1994 como una combinación de dos bases de datos en NIST: Special Database 1 and Special Database 3. Estas bases de datos consistían en dígitos escritos por estudiantes de preparatoria y empleados de la Oficina del Censo de los Estados Unidos, respectivamente.

3.3 Características

Algunas características de este dataset son:

Cuenta con 60,000 imágenes de entrenamiento y 10,000 imágenes de prueba.
- Cada imágen corresponde a un número en el rango [0,9]
- Las imágenes tienen un tamaño de 28x28x1

Este dataset se considera como "resuelto", ya que se ha logrado alcanzar tasas de error considerablemente pequeñas para este conjunto.

Es un conjunto "limpio", ya que los datos en este conjunto están ya limpias y curadas especialmente para entrenamiento.
- Si bien esto facilita el entrenamiento, no necesariamente representa una muestra representativa de la vida real.
- Las imagenes se encuentran centradas y normalizadas.

4. Desarrollo matemático del Problema

4.1 Explicación del problema y de la red neuronal

Podemos dividir el problema de reconocer dígitos escritos a mano en dos subproblemas. Primero, nos gustaría una forma de dividir una imagen que contiene muchos dígitos en una secuencia de imágenes separadas, cada una con un solo dígito. Por ejemplo, nos gustaría separar la siguiente imagen:

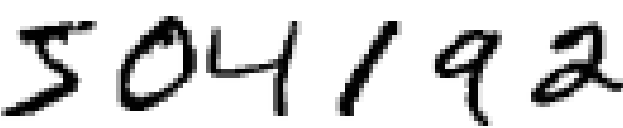
En 6 diferentres imágenes:

Los humanos resolvemos este problema de segmentación con facilidad, pero es un desafío para un programa de computadora dividir correctamente la imagen. Una vez que la imagen ha sido segmentada, el programa necesita clasificar cada dígito individual. Entonces, por ejemplo, nos gustaría que nuestro programa reconozca que el primer dígito de arriba,

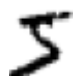
es un 5.

Nos concentraremos en escribir un programa para resolver el segundo problema, es decir, clasificar dígitos individuales. Hacemos esto porque resulta que el problema de segmentación no es tan difícil de resolver, una vez que tienes una buena forma de clasificar dígitos individuales. Hay muchos enfoques para resolver el problema de la segmentación. Un enfoque consiste en probar muchas formas diferentes de segmentar la imagen, utilizando el clasificador de dígitos individuales para puntuar cada segmentación de prueba. Una segmentación de prueba obtiene una puntuación alta si el clasificador de dígitos individuales confía en su clasificación en todos los segmentos, y una puntuación baja si el clasificador tiene muchos problemas en uno o más segmentos. La idea es que si el clasificador tiene problemas en alguna parte, probablemente tenga problemas porque la segmentación se eligió incorrectamente. Esta idea y otras variaciones se pueden utilizar para resolver bastante bien el problema de la segmentación. Entonces, en lugar de preocuparnos por la segmentación, nos concentraremos en desarrollar una red neuronal que pueda resolver el problema más interesante y difícil, a saber, reconocer dígitos escritos a mano individuales.

Para reconocer dígitos individuales usaremos una red neuronal de tres capas:

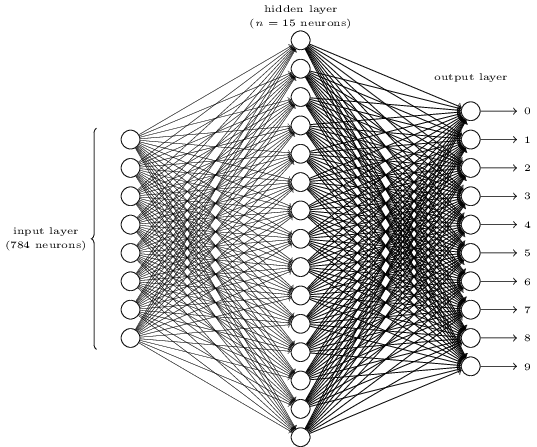
La capa de entrada de la red contiene neuronas que codifican los valores de los píxeles de entrada. Como se analiza en la siguiente sección, nuestros datos de entrenamiento para la red consistirán en muchas imágenes de dígitos escaneados escritos a mano de 28 x 28 pixeles, por lo que la capa de entrada contiene 784 = 28 x 28 neuronas. Los píxeles de entrada son en escala de grises, con un valor de 0 que representa el blanco, un valor de 1 que representa el negro y valores intermedios que representan sombras de gris que se oscurecen gradualmente.

La segunda capa de la red es una capa oculta. Denotamos el número de neuronas en esta capa oculta por , y experimentaremos con diferentes valores para n. El ejemplo que se muestra ilustra una pequeña capa oculta que contiene solo n = 15 neuronas.

La capa de salida de la red contiene 10 neuronas. Si la primera neurona se dispara, es decir, tiene una salida ≈1, eso indicará que la red cree que el dígito es un 0. Si la segunda neurona se dispara, eso indicará que la red cree que el dígito es un 1. Y así sucesivamente. . Con un poco más de precisión, numeramos las neuronas de salida del 0 al 9 y determinamos qué neurona tiene el valor de activación más alto. Si esa neurona es, digamos, la neurona número 6, entonces nuestra red adivinará que el dígito de entrada era un 6. Y así sucesivamente para las otras neuronas de salida.

4.2 Aplicando el descenso de gradiente

Usaremos la notación x para denotar los datos de entrada. Será conveniente considerar cada entrada de entrenamiento x como un vector dimensional de 28 x 28 = 784 dimensiones. Cada entrada en el vector representa el valor de gris para un solo píxel en la imagen. Denotaremos la salida deseada correspondiente por:

y = y(x)

donde y ds un vector de dimensión 10. Por ejemplo, si una imagen de entrenamiento en particular, x, muestra un 6, entonces:

y(x) = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0)^T

es la salida deseada de la red. Nótese que T representa la traspuesta, convirtiendo un vector fila en un vector ordinario (columna).

Lo que nos gustaría es un algoritmo que nos permita encontrar pesos y sesgos para que la salida de la red se aproxime a y(x) para todos las entradas de entrenamiento x. Para cuantificar qué tan bien estamos logrando este objetivo, definimos una función de costo:

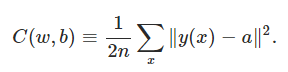
Aquí, w denota la colección de todos los pesos en la red, b todos los sesgos, n el nímero total de datos de entrenamiento, a es el vector de salidas de la red cuando x es la entrada, y la suma es sobre todas las entradas de entrenamiento x. Por supuesto, la salida a depende en x, w y b. La notación ∥v∥ denota la ongitud para un vector v

Llamaremos a C la función de coste cuadrática; a veces también se conoce como el error cuadrático medio o simplemente MSE.

Inspeccionando la función, vemos que

C(w,b)

es no negativa, ya que todos los términos de la suma son no negativos. Además, el costo C(w,b) se vuelve pequeño, es decir,

C(w,b) \approx 0

cuando y(x) es aproximadamente igual a la salida a por cada entrada x.

Por el contrario, no funciona tan bien cuando C(w,b) es grande; eso significaría que y(x) no está cerca de la salida a para una gran cantidad de entradas. Entonces, el objetivo de nuestro algoritmo de entrenamiento será minimizar el costo C(w,b) en función de los pesos y sesgos. En otras palabras, queremos encontrar un conjunto de pesos y sesgos que hagan que el costo sea lo más pequeño posible. Lo haremos usando un algoritmo conocido como descenso de gradiente.

Bien, supongamos que estamos tratando de minimizar alguna función, C(v). Esta podría ser cualquier función de valor real de muchas variables,

v = v_1, v_2, ...

Nótese que hemos reemplazado la notación w y b por v para enfatizar que esta podría ser cualquier función; ya no estamos pensando específicamente en el contexto de las redes neuronales. Para minimizar C(v), nos ayuda imaginar a C como una función de solo dos variables, a las que llamaremos v₁ y v₂

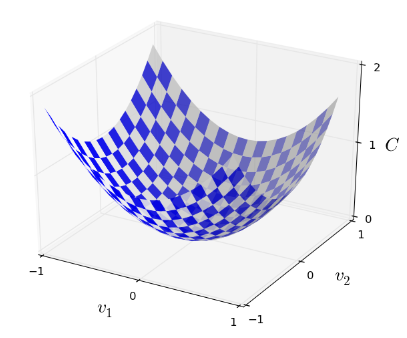
Lo que nos gustaría es encontrar dónde C alcanza su mínimo global. Ahora, por supuesto, para la función trazada arriba, podemos observar el gráfico y encontrar el mínimo. Una función general, C, puede ser una función complicada de muchas variables y, por lo general, no será posible simplemente observar el gráfico para encontrar el mínimo.

Una forma de atacar el problema es usar el cálculo para tratar de encontrar el mínimo analíticamente. Podríamos calcular derivadas y luego tratar de usarlas para encontrar lugares donde C es un extremo. Con un poco de suerte, eso podría funcionar cuando C es una función de solo una o unas pocas variables. Pero se convertirá en una pesadilla cuando tengamos muchas más variables. Y para las redes neuronales, a menudo queremos muchas más variables: las redes neuronales más grandes tienen funciones de costo que dependen de miles de millones de pesos y sesgos de una manera extremadamente complicada. Usar el cálculo para minimizar eso simplemente no funcionará.

Pensemos que tenemos una pelota sobre un valle, veamos qué es lo que sucede cuando movemos la pelota una pequeña cantidad Δv₁en la dirección v₁ y una pequeña cantidad Δv₂ en la dirección v₂. El cálculo nos dice que C cambia de la siguiente manera:

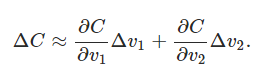
Vamos a encontrar una manera de elegir Δv₁ y Δv₂ para hacer ΔC negativo; es decir, los elegiremos para que la pelota ruede hacia el valle. Para descubrir cómo hacer esa elección, es útil definir Δv como el vector de cambios en v,

\Delta v = (\Delta v_1, \Delta v_2)^T

donde T es el operador de la traspuesta, convirtiendo vectores fila en vectores columna. También definiremos el gradiente de C como el vector de derivadas parciales,

(\frac{\partial C}{\partial v_1},\frac{\partial C}{\partial v_2})^T

Denotamos el vector gradiente por ∇ C

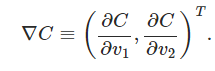
Con estas definiciones, la expresión de arriba se puede definir como,

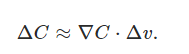
∇ C relaciona los cambios en v con los cambios en C, tal como esperaríamos que hiciera algo llamado gradiente. Pero lo realmente emocionante de la ecuación es que nos permite ver cómo elegir Δv para hacer que Δ C sea negativo. En particual, si elegimos

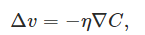
donde η es un parámetro positivo (conocido como el learning rate). Mediante los cambios de posición, vamos ir decreciendo a C hasta - esperemos - encontrar el mínimo global.

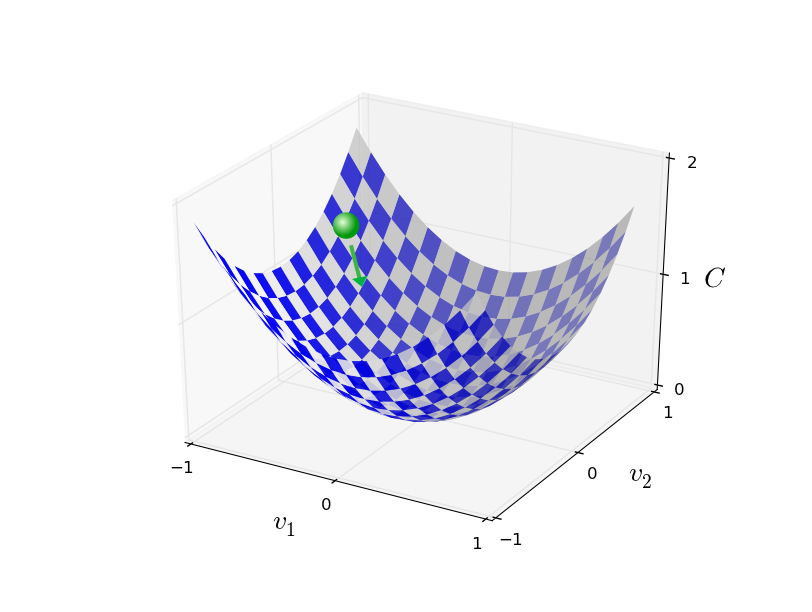
Resumiendo, la forma en que funciona el algoritmo de descenso del gradiente es calcular repetidamente el gradiente ∇ C y luego moverse en la dirección opuesta, "cayendo" por la pendiente del valle. Podemos visualizarlo así:

Referencias

Patterson, J., & Gibson, A. (2017). Deep Learning - A practitioner's Approach. O'Reilly.

Aggarwal, C. (2018). Neural Networks and Deep Learning. A Textbook